3059. Минимизация максимизатора
Компания ООО
Крис готовит к выпуску новое аппаратное устройство, которое называется
Максимизатор. Максимизатор имеет n
входов, пронумерованных от 1 до n. На
каждый вход подается одно целое число. Максимизатор имеет один выход,
представляющий собой наибольшее значение среди входов максимизатора.
Максимизатор
реализован как последовательность сортировщиков Sorter(i1, j1),
..., Sorter(ik, jk). Каждый сортировщик имеет
n входов и n выходов. Sorter(i, j) сортирует данные на входах i, i
+ 1, ..., j в неубывающем порядке, а
данные с остальных входов проходят на выход неизмененными. Выходом
максимизатора является n-ый выход его
последнего сортировщика.
Интерн (бывший
участник ACM) заметил, что из последовательности можно исключить некоторые
сортировщики так, чтобы максимизатор выдавал правильный результат. Найти длину
кратчайшей подпоследовательности сортировщиков, которые все еще выдают
правильные ответы для всех возможных комбинаций входных данных.
Вход. Состоит из нескольких тестов. Первая строка каждого теста
содержит два целых числа n и m (2 ≤ n ≤ 50000, 1 ≤ m
≤ 500000). Число n задает
количество входов, а m – количество
сортировщиков в последовательности. Начальное состояние сортировщиков
описывается следующими m строками. k-ая строка содержит параметры k-го сортировщика: два целых числа ik и jk (1 ≤ ik
< jk ≤ n).
Выход. Для каждого теста в отдельной строке вывести длину
кратчайшей подпоследовательности сортировщиков, выдающих тот же ответ, что и
исходная последовательность сортировщиков на всех возможных входных данных.
|
Пример
входа |
Пример
выхода |
|
40 6 20 30 1 10 10 20 20 30 15 25 30 40 |
4 |
РЕШЕНИЕ
структуры данных –
дерево отрезков + динамическое
программирование
Анализ алгоритма
01-принцип состоит в
следующем. Подадим на первый вход единицу, а на все остальные входы нули. Если
по окончанию работы сортировщиков на n-ом
выходе будет единица, а на всех остальных выходах нули, то сортировщики работают
корректно. То есть сортировщики должны быть способны перенести начальную
единицу на первом входе на n-ый
выход.
Заведем массив
dp длины n, где dp[i] равно минимальному количеству
сортировщиков, необходимых для сортировки чисел на входах 1 .. i. Положим dp[1] = 0. В остальные ячейки
массива dp изначально занесем INF (плюс бесконечность).
Рассмотрим
текущий сортировщик Sorter(ik,
jk). Если единица
находится в одной из позиций [ik,
jk – 1] (единица у нас
всегда одна, на остальных позициях всегда стоят нули), то он способет перенести
ее в jk-ую позицию. Это
означает что
dp[jk] = min(dp[jk], min(dp[ik], dp[ik + 1], …, dp[jk – 1]) + 1)
Остается
пересчитать значения для каждого сортировщика и вывести dp[n] (поскольку n –
наибольший номер выхода, то обязательно должен существовать сортировщик, конец
интервала которого равен n). Для избежания
лимита по времени минимум min(dp[ik],
dp[ik + 1], …, dp[jk – 1]) следует вычислять при помощи дерева отрезков.
Пример
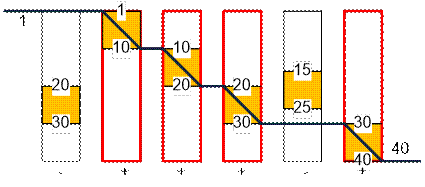
Реализация алгоритма
Объявим константы
и рабочие массивы.
#define INF 2100000000
#define MAX 50010
vector<int>
dp;
int SegTree[4*MAX];
Создание дерева
отрезков. Заносим в каждую вершину значение плюс бесконечность.
void build(int Vertex, int Left, int Right)
{
if (Left == Right)
SegTree[Vertex] = INF;
else
{
int Middle = (Left + Right) / 2;
build (2*Vertex, Left, Middle);
build (2*Vertex+1, Middle+1, Right);
SegTree[Vertex] = min(SegTree[2*Vertex],SegTree[2*Vertex+1]);
}
}
Устанавливаем dp[Position]
= NewValue.
void SetValue(int Vertex, int LeftPos, int
RightPos,
int
Position, int NewValue)
{
if (LeftPos == RightPos)
SegTree[Vertex] = NewValue;
else
{
int Middle = (LeftPos + RightPos) / 2;
if (Position <= Middle)
SetValue(2*Vertex, LeftPos, Middle, Position, NewValue);
else
SetValue(2*Vertex+1, Middle+1, RightPos, Position, NewValue);
SegTree[Vertex] = min(SegTree[2*Vertex],SegTree[2*Vertex+1]);
}
}
Вершине Vertex
соответствует интервал [LeftPos; RightPos]. Вычисляем минимум на отрезке [Left; Right].
int GetMin(int Vertex, int LeftPos, int
RightPos, int Left, int
Right)
{
if (Left > Right) return
INF;
if ((LeftPos == Left) && (RightPos == Right))
return SegTree[Vertex];
int Middle = (LeftPos + RightPos) / 2;
return min(GetMin(2*Vertex, LeftPos, Middle, Left,
min(Middle,Right)),
GetMin(2*Vertex+1, Middle+1, RightPos, max(Left,Middle+1), Right));
}
Основная часть
программы. Инициализируем массив dp. Строим дерево отрезков для интервала [1..n]. Дерево отрезков дублирует содержимое
массива dp.
scanf("%d
%d",&n,&m);
dp.assign(n+1,INF); dp[1] = 0;
build(1,1,n);
SetValue(1,1,n,1,0);
for(i = 0; i < m; i++)
{
scanf("%d %d",&l,&r);
Вычисляем min(dp[l],
dp[l + 1], …, dp[r – 1]).
int mn = GetMin(1,1,n,l,r-1);
Пересчитываем
dp[r] = min(dp[r], min(dp[l], dp[l + 1], …, dp[r – 1]) + 1)
dp[r] = min(dp[r],mn + 1);
Устанавливаем r-ый
элемент дерева отрезков равным dp[r].
SetValue(1,1,n,r,dp[r]);
}
Выводим ответ.
printf("%d\n",dp[n]);
Реализация линейная:
динамика без дерева отрезков, TLE.
#include <cstdio>
#include <vector>
#include <algorithm>
#define INF 2100000000
using namespace std;
int n, m, i, j, l, r;
vector<int>
dp;
int main(void)
{
scanf("%d %d",&n,&m);
dp.assign(n+1,INF); dp[1] = 0;
for(i = 0; i < m; i++)
{
scanf("%d %d",&l,&r);
int mn =
*min_element(&dp[l],&dp[r-1]);
dp[r] = min(dp[r],mn + 1);
}
printf("%d\n",dp[n]);
return 0;
}